Thermalization and Ergodicity
The dynamics of closed quantum systems has experience a renaissance in the last few years due to developments primarily in the physics of cold atomic gases. These systems are cooled and isolated from their environment, so that their behavior can be well approximated by the deterministic quantum evolution of the Schroedinger equation. Initial forays into the field of equilibration in such closed systems showed that many conventional statistical mechanical principles could be recovered by using the eigenstate thermalization hypothesis (ETH), which states that every many-body eigenstate at a given energy density behaves equivalently with respect to local observables [1]. However, soon after the ETH was proposed, an experiment involving a 1D Bose gas found sharp disagreement with this theory by imprinting the gas with a non-equilibrium momentum distribution that did not relax over experimental time scales [2]. This behavior was later traced back to the quantum integrability of the model, a fairly generic situation in one dimension where the number of conservation laws scales as the system size.
Related to the concept of thermalization is the idea of understanding dynamics for generic systems at high energy density (i.e., finite temperature, if they thermalize). In addition to integrability, it has been found that localization [3,4] of the many-body wave functions due to disorder can impede thermalization. Recent work on these many-body localized systems has uncovered phase transitions that occur not in thermodynamic quantities, but instead in dynamics within individual eigenstates. These transitions, called "eigenstate phase transitions" [5] or "Hilbert glass transitions" [6], appear to be a robust feature of certain localized models at high energy density.
We have found that such dynamic singularities can occur in the absence of disorder, in cases where the model is integrable. More specifically, we find for the transverse-field Ising model that a connected two-time correlation function related to the quantum metric tensor diverges at arbitrary temperature when the field is tuned close to the location of the zero-temperature critical point. By adding superlattice potentials that don't break integrability, we confirm that this dynamic divergence is robust. We are in the process of investigating how this divergence behaves in the presence of interactions, where we expect that the divergence would be lost due to the ETH.
Related to the concept of thermalization is the idea of understanding dynamics for generic systems at high energy density (i.e., finite temperature, if they thermalize). In addition to integrability, it has been found that localization [3,4] of the many-body wave functions due to disorder can impede thermalization. Recent work on these many-body localized systems has uncovered phase transitions that occur not in thermodynamic quantities, but instead in dynamics within individual eigenstates. These transitions, called "eigenstate phase transitions" [5] or "Hilbert glass transitions" [6], appear to be a robust feature of certain localized models at high energy density.
We have found that such dynamic singularities can occur in the absence of disorder, in cases where the model is integrable. More specifically, we find for the transverse-field Ising model that a connected two-time correlation function related to the quantum metric tensor diverges at arbitrary temperature when the field is tuned close to the location of the zero-temperature critical point. By adding superlattice potentials that don't break integrability, we confirm that this dynamic divergence is robust. We are in the process of investigating how this divergence behaves in the presence of interactions, where we expect that the divergence would be lost due to the ETH.
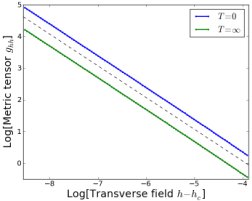
Figure: Divergence of the quantum metric tensor of the transverse-field Ising model near the field value h=1 that would correspond to the zero temperature quantum critical point. Up to a factor of 2, the metric diverges in an identical way at infinite temperature, despite the lack of any interesting equilibrium thermodynamic behavior of the system at infinite temperature.
References:
[1] M. Rigol, V. Dunjko, M. Olshanii. Nature 452, 854 (2008).
[2] T. Kinoshita, T. Wenger, D. S. Weiss. Nature 440, 900 (2006).
[3] D.M. Basko, I.L. Aleiner, B.L. Altshuler. Annals of Physics 321, 1126 (2006).
[4] A. Pal, D. A. Huse. Phys. Rev. B 82, 174411 (2010).
[5] D. A. Huse, R. Nandkishore, V. Oganesyan, A. Pal, S.L.Sondhi. Phys. Rev. B 88, 014206 (2013).
[6] D. Pekker, G. Refael, E. Altman, E. Demler, V. Oganesyan. Phys. Rev. X 4, 011052 (2014).
[1] M. Rigol, V. Dunjko, M. Olshanii. Nature 452, 854 (2008).
[2] T. Kinoshita, T. Wenger, D. S. Weiss. Nature 440, 900 (2006).
[3] D.M. Basko, I.L. Aleiner, B.L. Altshuler. Annals of Physics 321, 1126 (2006).
[4] A. Pal, D. A. Huse. Phys. Rev. B 82, 174411 (2010).
[5] D. A. Huse, R. Nandkishore, V. Oganesyan, A. Pal, S.L.Sondhi. Phys. Rev. B 88, 014206 (2013).
[6] D. Pekker, G. Refael, E. Altman, E. Demler, V. Oganesyan. Phys. Rev. X 4, 011052 (2014).
