Kibble-Zurek scaling
The Kibble-Zurek mechanism describes systems ramped slowly across a second-order critical point [1,2]. Due to critical slowing down, it is impossible to perform such a ramp adiabatically. As originally proposed by Kibble in the context of the early universe, and later generalized by Zurek in condensed matter systems, the time scale for breaking out of adiabaticity is set by the equilibrium scaling exponents of the model, leading to universal predictions for the number of topological defects (e.g., vortices in a superfluid) left over after such a ramping protocol.
Recent work [3,4] has suggested that this story can be extended further to an entire non-equilibrium critical scaling theory. The basic idea is that, in the vicinity of the critical point, the relevant time and length scales are set by the time and length scales below which the system appears adiabatic. These scales are straightforwardly connected to the ramp rate by power laws that depend only on the equilibrium critical exponents. Using these arguments, one finds that in the vicinity of the critical point we get universal dynamics, yielding predictions for observables at all times instead of just late-time defect densities.
In graduate school, I worked towards establishing the universality of Kibble-Zurek scaling, numerically showing that integrable and non-integrable models in the same equilibrium universality class display identical dynamics [5,6]. Recently, we have been working to extend this idea to cases where the field driving the system across the phase transition is imbued with dynamics of its own [7]. Then the critical slowing down of the spin system provides a back-action on the dynamic field, generally slowing down its motion. We find that, for a very general set of initial conditions, the field is dynamically trapped near the quantum critical point, since that's where the system has enough low-energy modes to absorb the kinetic energy of the field. We are investigating possible implications for this in condensed matter systems, as well as in high-energy physics, where a simplified model of inflation would suggest that this mechanism could lead to a light Higgs mass (as seen at the LHC) with less fine-tuning than some standard inflationary models.
Recent work [3,4] has suggested that this story can be extended further to an entire non-equilibrium critical scaling theory. The basic idea is that, in the vicinity of the critical point, the relevant time and length scales are set by the time and length scales below which the system appears adiabatic. These scales are straightforwardly connected to the ramp rate by power laws that depend only on the equilibrium critical exponents. Using these arguments, one finds that in the vicinity of the critical point we get universal dynamics, yielding predictions for observables at all times instead of just late-time defect densities.
In graduate school, I worked towards establishing the universality of Kibble-Zurek scaling, numerically showing that integrable and non-integrable models in the same equilibrium universality class display identical dynamics [5,6]. Recently, we have been working to extend this idea to cases where the field driving the system across the phase transition is imbued with dynamics of its own [7]. Then the critical slowing down of the spin system provides a back-action on the dynamic field, generally slowing down its motion. We find that, for a very general set of initial conditions, the field is dynamically trapped near the quantum critical point, since that's where the system has enough low-energy modes to absorb the kinetic energy of the field. We are investigating possible implications for this in condensed matter systems, as well as in high-energy physics, where a simplified model of inflation would suggest that this mechanism could lead to a light Higgs mass (as seen at the LHC) with less fine-tuning than some standard inflationary models.
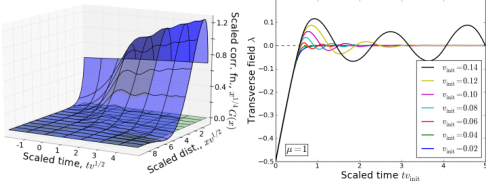
Left: Scaled correlation functions of the transverse-field Ising model during a Kibble-Zurek ramp. In addition to being universal, the dynamics show interesting non-thermal behavior.
Right: Demonstration of critical trapping. For slow enough initial velocities, the dynamic field is trapped at the critical point as predicted from an extension to Kibble-Zurek scaling.
References:
[1] T. Kibble. J. Phys. A 9, 1387 (1976).
[2] W. H. Zurek. Nature 317, 505 (1985).
[3] S. Deng, G. Ortiz, L. Viola. Europhys. Lett. 84, 67008 (2008).
[4] A. Chandran, A. Erez, S. S. Gubser, S. L. Sondhi. Phys. Rev. B 86, 064304 (2012).
[5] M. Kolodrubetz, D. Pekker, B. K. Clark, K. Sengupta. Phys. Rev. B, 85, 100505 (2012).
[6] M. Kolodrubetz, B. K. Clark, D. A. Huse. Phys. Rev. Lett. 109, 015701 (2012).
[7] M. Kolodrubetz, E. Katz, A. Polkovnikov. Phys. Rev. B 91, 054306 (2015).
[1] T. Kibble. J. Phys. A 9, 1387 (1976).
[2] W. H. Zurek. Nature 317, 505 (1985).
[3] S. Deng, G. Ortiz, L. Viola. Europhys. Lett. 84, 67008 (2008).
[4] A. Chandran, A. Erez, S. S. Gubser, S. L. Sondhi. Phys. Rev. B 86, 064304 (2012).
[5] M. Kolodrubetz, D. Pekker, B. K. Clark, K. Sengupta. Phys. Rev. B, 85, 100505 (2012).
[6] M. Kolodrubetz, B. K. Clark, D. A. Huse. Phys. Rev. Lett. 109, 015701 (2012).
[7] M. Kolodrubetz, E. Katz, A. Polkovnikov. Phys. Rev. B 91, 054306 (2015).
