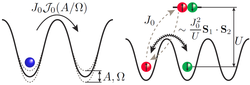
Periodically-driven systems
Periodic driving is on of the most important tools in the ultracold AMO toolkit. It allows for the creation of novel Hamiltonians that are not easily accessible in the solid state, from optical lattices to Harper-Hofstadter models. I am exploring these systems from both the engineering and the fundamental physics sides, i.e., the ways in which they are the same as their Hamiltonian counterparts and the interesting ways in which they can differ.
Periodic driving is on of the most important tools in the ultracold AMO toolkit. It allows for the creation of novel Hamiltonians that are not easily accessible in the solid state, from optical lattices to Harper-Hofstadter models. I am exploring these systems from both the engineering and the fundamental physics sides, i.e., the ways in which they are the same as their Hamiltonian counterparts and the interesting ways in which they can differ.
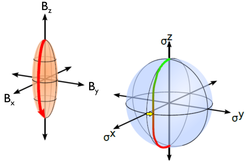
Geometry and dynamics
Quantum geometry describes how the wave function is modified upon changing parameters such as external control field and internal momentum. It is closely connected to dynamics. We have identified ways of measuring both the symmetric (metric) and anti-symmetric (Berry) parts of the geometric tensor using nearly-adiabatic protocols. Using these methods, we are working with experimentalists to measure topology in qubits.
Quantum geometry describes how the wave function is modified upon changing parameters such as external control field and internal momentum. It is closely connected to dynamics. We have identified ways of measuring both the symmetric (metric) and anti-symmetric (Berry) parts of the geometric tensor using nearly-adiabatic protocols. Using these methods, we are working with experimentalists to measure topology in qubits.
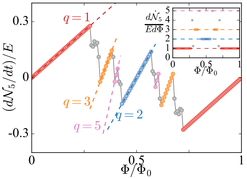
Controlled quantum systems
Quantum engineering allows one to realize fundamentally new regimes with no solid state analogue. Examples include Weyl semimetals in absurdly large magnetic fields (analogous to ~10,000 T in the solid state) and many-body spin chains in the presence of weak high-fidelity quantum measurement. Characterizing these new regimes leads to many surprising features, such as a fractal version of the chiral anomaly.
Quantum engineering allows one to realize fundamentally new regimes with no solid state analogue. Examples include Weyl semimetals in absurdly large magnetic fields (analogous to ~10,000 T in the solid state) and many-body spin chains in the presence of weak high-fidelity quantum measurement. Characterizing these new regimes leads to many surprising features, such as a fractal version of the chiral anomaly.
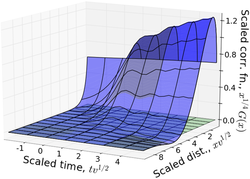
Kibble-Zurek scaling
When systems are ramped in the vicinity of a critical point, they undergo critical scaling similar to equilibrium systems. We have investigated a number of extensions to this phenomenon, including allowing the parameter tuning across the critical point to become dynamical. For such dynamic ramps, we've shown that the system is readily trapped near the phase transition.
When systems are ramped in the vicinity of a critical point, they undergo critical scaling similar to equilibrium systems. We have investigated a number of extensions to this phenomenon, including allowing the parameter tuning across the critical point to become dynamical. For such dynamic ramps, we've shown that the system is readily trapped near the phase transition.
Thermalization and ergodicity
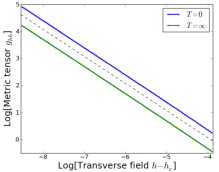
Quantum systems generically thermalize at the level of individual energy eigenstates in the absence of many-body localization or integrability, but ergodicity-breaking remains hard to see in for non-eigenstate wave functions. We have found a scenario where an integrable phase transition persists to infinite temperature and may be readily measured by dynamical response functions.
Quantum systems generically thermalize at the level of individual energy eigenstates in the absence of many-body localization or integrability, but ergodicity-breaking remains hard to see in for non-eigenstate wave functions. We have found a scenario where an integrable phase transition persists to infinite temperature and may be readily measured by dynamical response functions.
