Controlled quantum Systems
In addition to enabling the creation and control of interesting Hamiltonians, engineered quantum systems also enable one to explore new physics with no simple solid state analogue. This runs the gamut from the Bose-Hubbard model [1], a modern workhorse of ultracold atoms, to the BEC-BCS crossover in ultracold Fermi gases [2]. By keeping an eye on experimental developments in the field, my research searches for new regimes that these developments allow us to explore.
A recent example of this is our work to understand the chiral anomaly in cold atom realizations of Weyl semimetals [3]. The chiral anomaly describes the response of Weyl fermions to parallel electric and magnetic fields. In high-energy physics it was found to pump charge to/from a Weyl node at a rate proportional to the product of E and B. In the solid state, this has been predicted to lead to interesting transport effects such as negative magnetoresistance [4]. Cold atom proposals for realizing these novel topological semimetals in optical lattices (cf. [5]) naturally involve effective magnetic fields as well, but unlike their solid state counterparts, the Aharonov-Bohm phases imparted by effective magnetic fields in cold atoms are relatively large. This large-field regime was first explored in two-dimensional square lattices, giving rise to the famous Hofstadter butterfly [6]. However, at first blush the Hofstadter regime seems inconsistent with the chiral anomaly, since the chiral anomaly predicts a response linear in B, while lattice magnetic fields are required to be periodic in B upon inserting a flux quantum per unit cell by gauge invariance. We found that these limits could be rectified by starting off with a perfectly quantized chiral anomaly, which is then interrupted by a series of topological transitions to other quantized plateaus. These new plateaus can be connected to the emergence of new Weyl fermions at large flux, which in turn relates to topological properties of gap in the fractal butterfly energy structure. Crucially, while this part of phase space is entirely outside the regime of condensed matter experiments, it is naturally realized and readily measured in cold atoms.
Another unrelated example where engineered systems open new frontiers is in exploring quantum limits of measurement, which have become experimentally tractable recently with impressive technical developments in quantum information-preserving amplifiers. Using these novel tools to measure superconducting qubits, experimentalists here in Berkeley have measured individual quantum trajectories during the collapse process [7], sustained Rabi oscillations ad infinitum [8], and confirmed fundamental properties of the quantum Zeno effect [9]. Recent developments in their group and others have allowed such superconducting qubits to push towards the many-qubit regime, leaving open questions in many-body dynamics of weakly-measured systems. I have begun to explore symmetry breaking phenomena in this context. One interesting result that emerges is that weakly-measured systems can undergo a crossover between conventional Zeno freezing at strong measurement to many-body Zeno freezing at weak measurement, where the dynamics crosses over from being arrested by the measurement itself to being arrested by interactions. Interesting future work will involve understanding this crossover quantitatively and connecting it to the conventional theory of symmetry-broken phases.
A recent example of this is our work to understand the chiral anomaly in cold atom realizations of Weyl semimetals [3]. The chiral anomaly describes the response of Weyl fermions to parallel electric and magnetic fields. In high-energy physics it was found to pump charge to/from a Weyl node at a rate proportional to the product of E and B. In the solid state, this has been predicted to lead to interesting transport effects such as negative magnetoresistance [4]. Cold atom proposals for realizing these novel topological semimetals in optical lattices (cf. [5]) naturally involve effective magnetic fields as well, but unlike their solid state counterparts, the Aharonov-Bohm phases imparted by effective magnetic fields in cold atoms are relatively large. This large-field regime was first explored in two-dimensional square lattices, giving rise to the famous Hofstadter butterfly [6]. However, at first blush the Hofstadter regime seems inconsistent with the chiral anomaly, since the chiral anomaly predicts a response linear in B, while lattice magnetic fields are required to be periodic in B upon inserting a flux quantum per unit cell by gauge invariance. We found that these limits could be rectified by starting off with a perfectly quantized chiral anomaly, which is then interrupted by a series of topological transitions to other quantized plateaus. These new plateaus can be connected to the emergence of new Weyl fermions at large flux, which in turn relates to topological properties of gap in the fractal butterfly energy structure. Crucially, while this part of phase space is entirely outside the regime of condensed matter experiments, it is naturally realized and readily measured in cold atoms.
Another unrelated example where engineered systems open new frontiers is in exploring quantum limits of measurement, which have become experimentally tractable recently with impressive technical developments in quantum information-preserving amplifiers. Using these novel tools to measure superconducting qubits, experimentalists here in Berkeley have measured individual quantum trajectories during the collapse process [7], sustained Rabi oscillations ad infinitum [8], and confirmed fundamental properties of the quantum Zeno effect [9]. Recent developments in their group and others have allowed such superconducting qubits to push towards the many-qubit regime, leaving open questions in many-body dynamics of weakly-measured systems. I have begun to explore symmetry breaking phenomena in this context. One interesting result that emerges is that weakly-measured systems can undergo a crossover between conventional Zeno freezing at strong measurement to many-body Zeno freezing at weak measurement, where the dynamics crosses over from being arrested by the measurement itself to being arrested by interactions. Interesting future work will involve understanding this crossover quantitatively and connecting it to the conventional theory of symmetry-broken phases.
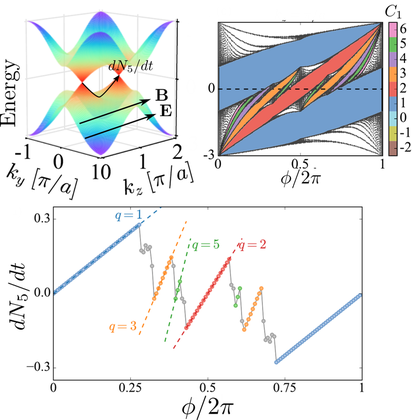
Top Left: Conventional chiral anomaly in a Weyl semimetal. Upon applying a parallel electric and magnetic fields, charge is pumped between Weyl nodes at a rate proportional to their product.
Top Right: Upon applying the large magnetic fields naturally realized in an optical lattice, the full energy spectrum forms a fractal pattern that is a 3D generalization of the Hofstadter butterfly. Data here is for a single momentum plane k=pi along the direction of the magnetic field. Magnetic field is represented by the Aharonov-Bohm phase picked up upon tunneling around a unit cell. Some of the gaps in the butterfly are colored by their topological Chern number.
Bottom: Rate of pumping between Weyl nodes as a function of magnetic flux with fixed electric field. The original chiral anomaly near zero field gives way to a (fractal) series of quantized slopes, which can be shown to emerge from the topological properties of gaps in the butterfly (top right).
References:
[1] M. Greiner, O. Mandel, T. Esslinger, T. W. Hansch, I. Bloch. Nature 415, 39 (2002).
[2] C. A. Regal, M. Greiner, D. S. Jin. Phys. Rev. Lett. 92, 040403 (2004).
[3] S. Roy, M. Kolodrubetz, J. E. Moore, A. G. Grushin. arXiv:1605.08445 (2016).
[4] D. T. Son and B. Z. Spivak. Phys. Rev. B 88, 104412 (2013).
[5] T. Dubcek, C. J. Kennedy, L. Lu, W. Ketterle, M. Soljacic, H. Buljan. Phys. Rev. Lett. 114, 225301 (2015).
[6] D. R. Hofstadter. Phys. Rev. B 14, 2239 (1976).
[7] K. W. Murch, S. J. Weber, C. Macklin, I. Siddiqi. Nature 502, 211 (2013).
[8] R. Vijay, C. Macklin, D. H. Slichter, S. J. Weber, K. W. Murch, R. Naik, A. N. Korotkov, I. Siddiqi. Nature 490, 77 (2012).
[9] D. H. Slichter, C. Muller, R. Vijay, S. J. Weber, A. Blais, I. Siddiqi. New J. Phys. 18, 053031 (2016).
[1] M. Greiner, O. Mandel, T. Esslinger, T. W. Hansch, I. Bloch. Nature 415, 39 (2002).
[2] C. A. Regal, M. Greiner, D. S. Jin. Phys. Rev. Lett. 92, 040403 (2004).
[3] S. Roy, M. Kolodrubetz, J. E. Moore, A. G. Grushin. arXiv:1605.08445 (2016).
[4] D. T. Son and B. Z. Spivak. Phys. Rev. B 88, 104412 (2013).
[5] T. Dubcek, C. J. Kennedy, L. Lu, W. Ketterle, M. Soljacic, H. Buljan. Phys. Rev. Lett. 114, 225301 (2015).
[6] D. R. Hofstadter. Phys. Rev. B 14, 2239 (1976).
[7] K. W. Murch, S. J. Weber, C. Macklin, I. Siddiqi. Nature 502, 211 (2013).
[8] R. Vijay, C. Macklin, D. H. Slichter, S. J. Weber, K. W. Murch, R. Naik, A. N. Korotkov, I. Siddiqi. Nature 490, 77 (2012).
[9] D. H. Slichter, C. Muller, R. Vijay, S. J. Weber, A. Blais, I. Siddiqi. New J. Phys. 18, 053031 (2016).
