Periodically-Driven Systems
One of the most powerful tools in engineered quantum systems, from ultracold AMO setups to systems of qubits, is periodic driving [1]. The key insight is encoded in Floquet's theorem, which says that time evolution in the presence of a periodic drive can be broken up into a "slow" part governed by a static effective Hamiltonian and a "fast" or "micromotion" part that describes dynamics within a period. Floquet engineering is the study of how to manufacture novel effective Hamiltonians that realize physics not easily accessible in equilibrium, from effective gauge fields to such simple tools of quantum optics as the optical lattice.
I have worked on many aspect of Floquet systems, from engineering new Hamiltonians to understanding what fundamental properties of Floquet systems differ from their static counterparts. On the engineering front, I have recently collaborated with Marin Bukov and Anatoli Polkovnikov at BU to explore strongly-driven strongly-interacting protocols [2]. Strong interactions are generally difficult to reconcile with Floquet physics because they lead to strong heating effects. We have shown that for strong resonant driving, this can be avoided, and indeed that the long time dynamics can be captured by a generalized version of the traditional Schrieffer-Wolff transform. This yields interesting strongly-interacting Hamiltonians including an unusual point in phase space where strong driving and interactions collude to yield a free fermionic Hamiltonian.
Another aspect of Floquet systems that makes them so interesting is their micromotion, which is often neglected in describing these systems. Much of my work focuses on the ways in which this micromotion distinguishes Floquet systems from their static counterparts. For instance, recent work has shown that micromotion can lead to novel topological invariants [3,4,5] and I have been working to understand what physically-measurable responses these topological invariants yield. At a more practical level, in Floquet systems one must not just realize a given effective Hamiltonian, but also figure out how to prepare it in the desired eigenstates. In collaboration with a group of grad students and postdocs at BU, I have helped extend methods of adiabatic perturbation theory to these driven systems [6], showing their validity for a wide range of models and exploring the connection to (Floquet) quantum geometry. One crucial effect that occurs in Floquet systems is resonances, which Hone et al. proved should inevitably destroy adiabaticity in Floquet systems [7]. We have shown that while this is formally true, there remain wide regions in parameter space where our perturbative description is valid, and furthermore that its breakdown due to resonances is deeply connected to the breakdown of another important tool in Floquet theory: the high-frequency expansion.
My other recent work in Floquet systems includes applying these ideas to ARPES experiments [8], where experimentalists have recently seen Floquet sidebands in driven surface states of topological insulators [9]. We simulate this experimental setup including the effects of the pulsed driving laser with finite penetration depth and find coherent oscillations of the electrons between the bulk and surface states induced by resonances with the drive. This signal bears a striking resemblance to recent experimental results. By connecting our model to the Demkov-Osherov model of many-level Landau-Zener crossings, we have been able to predict how the signal should change upon modifying the drive strength, frequency, or pulse length. This further enables us to argue that these resonant bulk-surface couplings should be universally seen in systems with gapless surface states driven resonantly with a gapped bulk, an increasingly common feature of topological materials.
I have worked on many aspect of Floquet systems, from engineering new Hamiltonians to understanding what fundamental properties of Floquet systems differ from their static counterparts. On the engineering front, I have recently collaborated with Marin Bukov and Anatoli Polkovnikov at BU to explore strongly-driven strongly-interacting protocols [2]. Strong interactions are generally difficult to reconcile with Floquet physics because they lead to strong heating effects. We have shown that for strong resonant driving, this can be avoided, and indeed that the long time dynamics can be captured by a generalized version of the traditional Schrieffer-Wolff transform. This yields interesting strongly-interacting Hamiltonians including an unusual point in phase space where strong driving and interactions collude to yield a free fermionic Hamiltonian.
Another aspect of Floquet systems that makes them so interesting is their micromotion, which is often neglected in describing these systems. Much of my work focuses on the ways in which this micromotion distinguishes Floquet systems from their static counterparts. For instance, recent work has shown that micromotion can lead to novel topological invariants [3,4,5] and I have been working to understand what physically-measurable responses these topological invariants yield. At a more practical level, in Floquet systems one must not just realize a given effective Hamiltonian, but also figure out how to prepare it in the desired eigenstates. In collaboration with a group of grad students and postdocs at BU, I have helped extend methods of adiabatic perturbation theory to these driven systems [6], showing their validity for a wide range of models and exploring the connection to (Floquet) quantum geometry. One crucial effect that occurs in Floquet systems is resonances, which Hone et al. proved should inevitably destroy adiabaticity in Floquet systems [7]. We have shown that while this is formally true, there remain wide regions in parameter space where our perturbative description is valid, and furthermore that its breakdown due to resonances is deeply connected to the breakdown of another important tool in Floquet theory: the high-frequency expansion.
My other recent work in Floquet systems includes applying these ideas to ARPES experiments [8], where experimentalists have recently seen Floquet sidebands in driven surface states of topological insulators [9]. We simulate this experimental setup including the effects of the pulsed driving laser with finite penetration depth and find coherent oscillations of the electrons between the bulk and surface states induced by resonances with the drive. This signal bears a striking resemblance to recent experimental results. By connecting our model to the Demkov-Osherov model of many-level Landau-Zener crossings, we have been able to predict how the signal should change upon modifying the drive strength, frequency, or pulse length. This further enables us to argue that these resonant bulk-surface couplings should be universally seen in systems with gapless surface states driven resonantly with a gapped bulk, an increasingly common feature of topological materials.
|
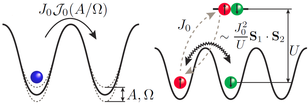
Top: Illustration of the basic connection between high-frequency expansions of periodically-driven systems (left) and the Schrieffer-Wolff transformation (right). In both cases, high-energy/fast-oscillatory terms are integrated out to leave an effective low-energy theory.
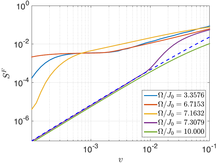
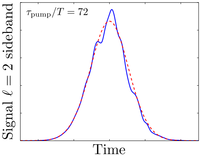
Bottom Left: Entropy of a periodically-driven many-body system after ramping up the drive at rate v starting from an undriven eigenstate . In the limit of slow ramps (v->0), one expects to wind up in a Floquet eigenstate at zero entropy, with leading non-adiabatic corrections shown by the blue dashed line. For small enough frequencies this picture breaks due to resonances, which make Floquet systems unique. Bottom Right: Simulated signal strength in the second Floquet sideband in the driven surface of a topological insulator (solid blue) compared to the "adiabatic" signal (dashed red). The different comes from coherent oscillations between surface and bulk states that survive in the thermodynamic limit. |
References:
[1] M. Bukov, L. D'Alessio, A. Polkovnikov. Advances in Physics, 64, 139 (2015).
[2] M. Bukov, M. Kolodrubetz, A. Polkovnikov. Phys. Rev. Lett. 116, 125301 (2016).
[3] T. Kitagawa, E. Berg, M. Rudner, E. Demler. Phys. Rev. B 82, 235114 (2010).
[4] M. Rudner, N. Lindner, E. Berg, M. Levin. Phys. Rev. X 3, 031005 (2013).
[5] R. Roy and F. Harper. arXiv:1603.06944 (2016).
[6] P. Weinberg, M. Bukov, L. D'Alessio, A. Polkovnikov, S. Vajna, M. Kolodrubetz. arXiv:1606.02229 (2016).
[7] D. W. Hone, R. Ketzmerick, W. Kohn. Phys. Rev. A 56, 4045 (1997).
[8] Y. H. Wang, H. Steinberg, P. Jarillo-Herrero and N. Gedik. Science 342, 453 (2013).
[9] M. Kolodrubetz, B. M. Fregoso, J. Moore. arXiv:1606.03459 (2016).
[1] M. Bukov, L. D'Alessio, A. Polkovnikov. Advances in Physics, 64, 139 (2015).
[2] M. Bukov, M. Kolodrubetz, A. Polkovnikov. Phys. Rev. Lett. 116, 125301 (2016).
[3] T. Kitagawa, E. Berg, M. Rudner, E. Demler. Phys. Rev. B 82, 235114 (2010).
[4] M. Rudner, N. Lindner, E. Berg, M. Levin. Phys. Rev. X 3, 031005 (2013).
[5] R. Roy and F. Harper. arXiv:1603.06944 (2016).
[6] P. Weinberg, M. Bukov, L. D'Alessio, A. Polkovnikov, S. Vajna, M. Kolodrubetz. arXiv:1606.02229 (2016).
[7] D. W. Hone, R. Ketzmerick, W. Kohn. Phys. Rev. A 56, 4045 (1997).
[8] Y. H. Wang, H. Steinberg, P. Jarillo-Herrero and N. Gedik. Science 342, 453 (2013).
[9] M. Kolodrubetz, B. M. Fregoso, J. Moore. arXiv:1606.03459 (2016).