Geometry and Dynamics
Consider a spin system in a magnetic field that is initialized in its ground state. When the magnetic field is varied slowly, the system follows adiabatically in its ground state, picking up a dynamical phase factor that is given by the time integral of the ground state energy. However, Berry [1] (and earlier Pancharatnam [2]) famously showed that there is an additional contribution to the phase, given by the non-trivial phase of the overlap between ground states at different fields. This connection between the ground states can be visualized as an effective vector potential, the curl of which yields an effective magnetic field known as the Berry curvature.
Similar to a standard magnetic field, the Berry curvature influences the dynamics of the probe field, inducing an effective Lorentz force that "back-acts" on the field. If we imagine the probe field as a test particle with some charge, then we could measure the Berry curvature by simply measuring the deflection due to this magnetic force, an idea which is, for example, at the heart of the "effective field" correction to Born-Oppenheimer approximation to molecular dynamics [3]. If instead the probe field is externally controlled, Gritsev et al. [4] showed that the effective force appears as a magnetization, which again can be measured experimentally.
We have used this idea [5,6] to measure the Berry curvature of superconducting qubits, in collaboration with the Lehnert group at JILA and the Martinis group at UCSB. Using their qubit architecture - a single 3D transmon at JILA and coupled gmons at UCSB - we ramp the effective magnetic field acting on these qubit systems and do tomography to measure the non-adiabatic magnetization response. If we think of the Berry curvature as an effective B-field, then by Gauss's law its surface integral gives the net magnetic monopole charge enclosed; this turns out to be a topologically-protected integer known as the first Chern number, which in electronic systems is responsible for the quantized conductance of the integer quantum Hall effect. In these qubit systems, we use such a non-adiabatic probe to measure the topological phase diagram as the interaction and fields are varied, providing a nice demonstration of topology in highly-tunable systems.
We are continuing to explore dynamical and topological effects of the Berry curvature, including experimentally visualizing magnetic monopoles. Furthermore, I have recently shown that these ideas can be directly extended to measure the second Chern number [7], which uniquely characterizes certain higher-dimensional systems with time-reversal symmetry [8]. The second Chern number characterizes rotations within a degenerate ground state manifold rather than simply the Abelian phase, and is thus a measure of non-Abelian physics. It is precisely these non-Abelian properties that are sought in in novel quasiparticles such as anyons and parafermions, which serve as a potential basis for topological quantum computation.
Similar to a standard magnetic field, the Berry curvature influences the dynamics of the probe field, inducing an effective Lorentz force that "back-acts" on the field. If we imagine the probe field as a test particle with some charge, then we could measure the Berry curvature by simply measuring the deflection due to this magnetic force, an idea which is, for example, at the heart of the "effective field" correction to Born-Oppenheimer approximation to molecular dynamics [3]. If instead the probe field is externally controlled, Gritsev et al. [4] showed that the effective force appears as a magnetization, which again can be measured experimentally.
We have used this idea [5,6] to measure the Berry curvature of superconducting qubits, in collaboration with the Lehnert group at JILA and the Martinis group at UCSB. Using their qubit architecture - a single 3D transmon at JILA and coupled gmons at UCSB - we ramp the effective magnetic field acting on these qubit systems and do tomography to measure the non-adiabatic magnetization response. If we think of the Berry curvature as an effective B-field, then by Gauss's law its surface integral gives the net magnetic monopole charge enclosed; this turns out to be a topologically-protected integer known as the first Chern number, which in electronic systems is responsible for the quantized conductance of the integer quantum Hall effect. In these qubit systems, we use such a non-adiabatic probe to measure the topological phase diagram as the interaction and fields are varied, providing a nice demonstration of topology in highly-tunable systems.
We are continuing to explore dynamical and topological effects of the Berry curvature, including experimentally visualizing magnetic monopoles. Furthermore, I have recently shown that these ideas can be directly extended to measure the second Chern number [7], which uniquely characterizes certain higher-dimensional systems with time-reversal symmetry [8]. The second Chern number characterizes rotations within a degenerate ground state manifold rather than simply the Abelian phase, and is thus a measure of non-Abelian physics. It is precisely these non-Abelian properties that are sought in in novel quasiparticles such as anyons and parafermions, which serve as a potential basis for topological quantum computation.
|
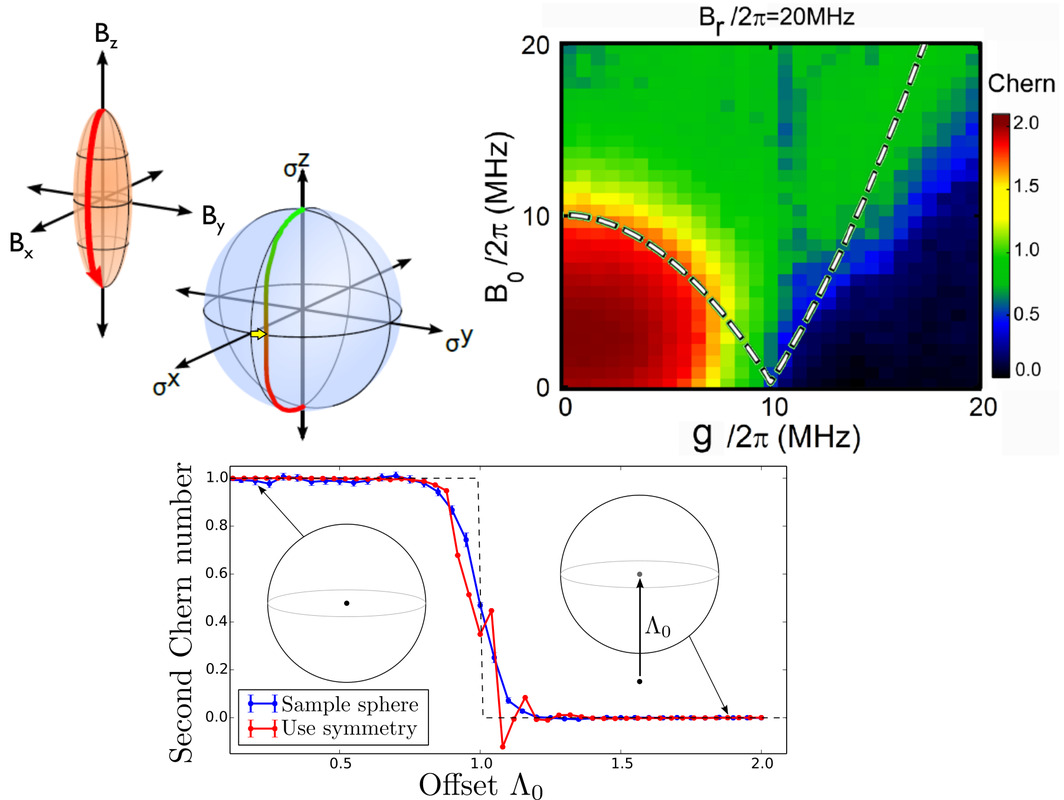
Top Left: As a parameter is slowly varied - say the magnetic field on a qubit - the deflection of the system from its adiabatic path (yellow arrow) gives information about the Berry curvature. Top Right: We have used this technique to measure the Berry curvature of two interacting qubits in an effective magnetic field. Here I show the experimental topological phase diagram for such a system, where the Chern number is defined with respect to the spherical angles of the external field. See Ref. [6] for more details. Bottom: Similar ideas can be applied to measure the second Chern number, the leading non-Abelian topological invariant. This loosely involves taking this linear response and "squaring" it to remove the Abelian component. An open question is whether non-Abelian physics can be directly measured through higher-order non-adiabatic corrections. |
References:
[1] M. V. Berry, Proc. Roy. Soc. A 392, 45 (1984).
[2] S. Pancharatnam, Proceedings of the Indian Academy of Science A 44, 247262 (1956).
[3] Shapere, A. and Wilczek, F. Geometric Phases in Physics. World Scientific, Singapore (1989).
[4] V. Gritsev and A. Polkovnikov, Proceedings of the National Academy of Sciences 109, 6457 (2012).
[5] M. D. Schroer, M. H. Kolodrubetz, W. F. Kindel, M. Sandberg, J. Gao, M. R. Vissers, D. P. Pappas, A. Polkovnikov, K. W. Lehnert. Phys. Rev. Lett. 113, 050402 (2014).
[6] P. Roushan, C. Neill, Y. Chen, M. Kolodrubetz, C. Quintana, N. Leung, M. Fang, R. Barends, B. Campbell, Z. Chen, B. Chiaro, A. Dunsworth, E. Jeffrey, J. Kelly, A. Megrant, J. Mutus, P. J. J. O’Malley, D. Sank, A. Vainsencher, J. Wenner, T. White, A. Polkovnikov, A. N. Cleland, J. M. Martinis. Nature 515, 241 (2014).
[7] M. Kolodrubetz. Phys. Rev. Lett. 117, 015301 (2016).
[8] J. E. Avron, L. Sadun, J. Segert, B. Simon. Communications in Mathematical Physics 124, 595 (1989).
[1] M. V. Berry, Proc. Roy. Soc. A 392, 45 (1984).
[2] S. Pancharatnam, Proceedings of the Indian Academy of Science A 44, 247262 (1956).
[3] Shapere, A. and Wilczek, F. Geometric Phases in Physics. World Scientific, Singapore (1989).
[4] V. Gritsev and A. Polkovnikov, Proceedings of the National Academy of Sciences 109, 6457 (2012).
[5] M. D. Schroer, M. H. Kolodrubetz, W. F. Kindel, M. Sandberg, J. Gao, M. R. Vissers, D. P. Pappas, A. Polkovnikov, K. W. Lehnert. Phys. Rev. Lett. 113, 050402 (2014).
[6] P. Roushan, C. Neill, Y. Chen, M. Kolodrubetz, C. Quintana, N. Leung, M. Fang, R. Barends, B. Campbell, Z. Chen, B. Chiaro, A. Dunsworth, E. Jeffrey, J. Kelly, A. Megrant, J. Mutus, P. J. J. O’Malley, D. Sank, A. Vainsencher, J. Wenner, T. White, A. Polkovnikov, A. N. Cleland, J. M. Martinis. Nature 515, 241 (2014).
[7] M. Kolodrubetz. Phys. Rev. Lett. 117, 015301 (2016).
[8] J. E. Avron, L. Sadun, J. Segert, B. Simon. Communications in Mathematical Physics 124, 595 (1989).